Tableaux de signes - Inéquations --- Introduction ---

Ce module regroupe pour l'instant 14 exercices sur les études de signe et la résolution d'inéquations (niveau Seconde, Lycée).

Associer tableau et expressions

De quelle(s) expression(s) le tableau suivant est-il le tableau de signes ?

Il peut y avoir plusieurs réponses ou aucune.

Inéquation particulière

On peut résoudre l'inéquation (I)     sans tableau de signes, car le signe de est évident.

L'ensemble des solutions de l'inéquation (I) est alors :

.

Inéquation avec quotient

Résoudre algébriquement sur l'inéquation (1) :
  1. L'inéquation (1) équivaut à l'inéquation avec et les binômes du premier degré suivants :
    = et = .
    On a montré que résoudre (1) équivaut à résoudre l'inéquation (2) : .
  2. On étudie le signe du quotient en fonction de . On obtient le tableau suivant :
  3. On définit les ensembles suivants : D'après le tableau de signe, l'ensemble des solutions de (1) et (2) est :
    .

Inéquation avec quotient (2)

Résoudre algébriquement sur l'inéquation (1) : .
  1. L'inéquation (1) équivaut à l'inéquation suivante :
    = (forme développée).
    = (forme factorisée).
    On a montré que résoudre (1) équivaut à résoudre l'inéquation (2) :
  2. Faire sur papier libre l'étude des signes du quotient .
    Ensuite, dans la liste suivante, cocher tous les intervalles, dont la réunion est l'ensemble des solutions de l'inéquation (1) :

Inéquation avec quotient (3)

Résoudre algébriquement sur l'inéquation (1) : .
  1. L'inéquation (1) équivaut à l'inéquation (2) suivante :
    avec = (donner la forme développée).
    On a montré que résoudre (1) équivaut à résoudre l'inéquation (2) :     0.
  2. On peut réécrire le numérateur sous forme canonique :

    = = avec .

  3. L'inéquation (1) équivaut donc aussi à l'inéquation (3) :     0.
  4. Que peut-on dire du numérateur ?

  5. On constate que le numérateur ne se factorise pas et garde un signe constant. On constate que le numérateur se factorise en .
  6. Faire sur papier libre l'étude des signes du quotient   .
    Ensuite, dans la liste suivante, cocher tous les intervalles, dont la réunion est l'ensemble des solutions de l'inéquation (1) :

Inéquation évidente

On peut résoudre l'inéquation (I)     sans tableau de signe, car le signe de est évident. L'ensemble des solutions de (I) est alors :

.

Vérifier un tableau de signes (1)

Un élève a dressé le tableau suivant pour étudier le signe de la fonction définie par :
Ce tableau est-il correct ? Sinon, quelle erreur a été commise ?

Vérifier un tableau de signes (2)

Un élève a dressé le tableau suivant pour étudier le signe de la fonction définie par :
A-t-il raison ? Sinon, cochez toutes les erreurs qu'il a commises.

Signe d'un binôme ax+b

Complétez le tableau de signes du binôme du premier degré .

Expression de signe évident

L'expression a un signe évident quel que soit le réel est toujours .

Lecture graphique

La représentation graphique d'une fonction , définie sur = [- ,] [- ,[ cup ] , ] , est donnée dans le repère (O ; I, J) ci-contre. On admet que la fonction ne change pas de sens de variation en dehors du graphique.
Répondre aux questions suivantes par lecture graphique.

  1. Combien l'équation a-t-elle de solutions dans ?
  2. L'équation n'a aucune solution dans .
  3. Compléter le tableau de signes de
-
  • L'équation n'admet aucune solution dans .
    La fonction n'est pas définie en .
  • Compléter le tableau de signes de - ||
  • L'équation a une unique solution 1 dans .
    La valeur arrondie au dixième de 1 est .
  • Compléter le tableau de signes de - 0
  • L'équation a une unique solution 1 dans . La fonction n'est pas définie en .
    La valeur arrondie au dizième de 1 est : .
  • Compléter le tableau de signes de -   0 ||
  • L'équation a une unique solution 1 dans . La fonction n'est pas définie en .
    La valeur arrondie au dizième de 1 est : .
  • Compléter le tableau de signes de -   || 0
  • L'équation a deux solutions 1 et 2 dans .
    Les valeurs arrondies de 1 et 2 sont respectivement : et .
  • Compléter le tableau de signes de -   0 0
  • L'équation a trois solutions 1, 2 et 3 dans .
    Les valeurs arrondies au dixième de , et sont respectivement : , et .
  • Compléter le tableau de signes de -     0 0 0
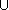
    • xrange -, yrange , parallel -,,-,,1,0, 2*+1, grey parallel -,,,,0,1, (-)++1, grey hline 0,0,black vline 0,0,black arrow 0,0,1,0,8, black arrow 0,0,0,1,8, black text black , -0.5,-0.2,small , O text black , 1,-0.3,small , I text black , -0.5,1,small , J linewidth 1.5 plot blue,

    Signe d'un produit ou quotient

    Étudier en fonction de le signe du produit quotient .

    Signe d'une fonction produit ou quotient

    Construire le tableau de signes de la fonction définie sur , pour tout réel tel que , par .

    Signe d'une expression a + u(x)/v(x)

    Étudier en fonction de le signe de l'expression .
    Compléter le tableau ci-dessous.

    The most recent version
    Cette page n'est pas dans son apparence habituelle parce que WIMS n'a pas pu reconnaître votre navigateur web.
    Afin de tester le navigateur que vous utilisez, veuillez taper le mot wims ici : puis appuyez sur ``Entrer''.

    Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.

    • Description: étude de signes et résolution algébrique d'inéquation (en Seconde). interactive exercises, online calculators and plotters, mathematical recreation and games
    • Keywords: interactive mathematics, interactive math, server side interactivity, algebra,, inequations,sign,factorization,roots,
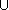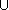