Ensembles

Objectifs et conseils

Ce cours est une introduction à la théorie des ensembles. Ensuite, pour les fonctions et les applications, consultez le cours Doc Fonctions, applications

Définitions
Opérations sur les ensembles
Cardinal
- Cardinal
- Cardinaux : exercices pratiques

Ensembles

Définition "intuitive". On dit, traditionnellement, qu'un ensemble, noté par exemple $E$ , est une collection, un regroupement d'objets appelés éléments.

Notations. L'assertion " $a$ appartient à $E$ '' se note $a \in E$ . L'assertion " $b$ n'appartient pas à $E$ '' se note $b \notin E$ .

Un ensemble peut se définir

soit en extension : en donnant la liste de tous ses éléments, si c'est possible, souvent entre deux accolades, par exemple $E = {a, b, c}$ .
soit en compréhension en donnant une propriété qui caractérise ses éléments, par exemple $F$ est l'ensemble des entiers pairs.

En particulier, un ensemble à un seul élément $a$ est appelé un singleton, noté alors ${a}$ .

Exemples d'ensembles.

]1,3], $ℝ^{n}$ , $ℚ$ , les irrationnels, les solutions d'une équation...
${(x, y) \in ℝ^{2}, y \neq x^{2}}$ .
L'ensemble des termes d'une suite $(u_{n})_{n \in ℕ}$ . Il est noté ${u_{n}, n \in ℕ}$ .
Le graphe d'une application $f$ d'un ensemble $E$ dans un ensemble $F$ , c'est-à-dire l'ensemble $G = {(x, f (x)), x \in E}$

Ensemble vide, sous-ensemble

Définition 1. Disons qu'on peut parler d'ensemble dès que l'on peut dire si un objet est (ou non) élément de cet ensemble... Ceci permet de définir plus aisément l'ensemble vide, noté traditionnellement

\emptyset

(la lettre grecque phi majuscule), comme étant celui qui n'a pas d'élément ou, mieux, celui auquel aucun objet n'appartient...

Définition 2. Un ensemble

E

est inclus (contenu) dans un ensemble

F

si tout élément de

E

est aussi un élément de

F

. On dit alors que

E

est un sous-ensemble ou une partie de

F

et on note

E \subset F

Remarques.

Les inclusions $E \subset E$ et $\emptyset \subset E$ sont évidentes.
$\emptyset$ est inclus dans tout ensemble.

Exercices

Appartenance/inclusion : ensembles d'entiers 1
Intervalles
Appartenance/inclusion : ensembles d'entiers 2

Produit cartésien, partition

Définition. On appelle produit cartésien de deux ensembles

A

B

l'ensemble, noté

A \times B

, défini par :

$A \times B = {(x, y) ∣ x \in A$ et $y \in B}$

Le produit cartésien $A \times B$ , avec $A =$ [1 , 4 ] et $B$ = [2 , 6 ] est la partie grise de cette représentation graphique.

On généralise cette définition au produit cartésien de $n$ ensembles $A_{1}, A_{2}, A_{3}, \dots, A_{n}$ :

$A_{1} \times A_{2} \times A_{3} \times \dots \times A_{n} = {(x_{1}, x_{2}, \dots, x_{n}) ∣ x_{i} \in A_{i} pour 1 \leq i \leq n}$

Exercices

Produit cartésien 1
Produit cartésien 2
Produits cartésien de trois ensembles

Partition d'un ensemble

Définition. On appelle partition d'un ensemble

E

la donnée de

n

sous-ensembles

A_{i}

E

pour

1 \leq i \leq n

, tels que :

$\forall i, 1 \leq i \leq n, A_{i} \neq \emptyset$
$A_{i} \cap A_{j} = \emptyset (i \neq j)$
$A_{1} \cup A_{2} \cup A_{3} \cup \dots \cup A_{n} = E$

Exemples de partitions.

Pour $E = {1, 2, 3}$ , il n'existe que 5 partitions possibles : ${{1}, {2}, {3}}, {{1, 2}, {3}}, {{1, 3}, {2}}, {{1}, {2, 3}} et {{1, 2, 3}}$
Pour $E = ℝ^{2}$ , voici un exemple de partition, formée de trois parties : ${{(x, y) \in ℝ^{2}, tels que y = x^{2}}, {(x, y) \in ℝ^{2}, tels que y < x^{2}}, {(x, y) \in ℝ^{2}, tels que y > x^{2}}}$
Pour $E = ℝ$ , la partition : ${[n, n + 1 [, n \in ℕ}$ est constituée d'une infinité de parties.

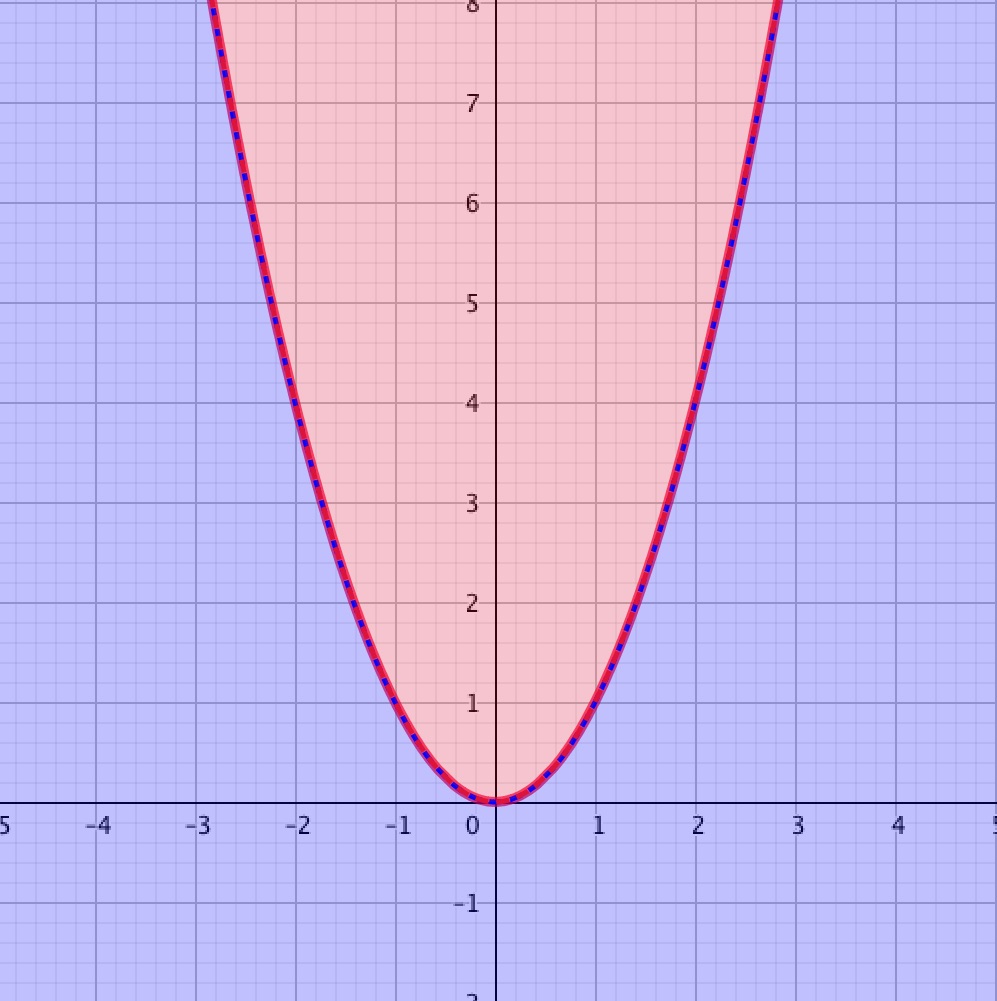
La figure ci-dessous est une représentation graphique d'une partition de $[- 5, 5] \times [- 2, 8]$ , comme dans l'exemple 2.

La partie { $(x, y) \in ℝ^{2}, tels que y = x^{2}}$ (la courbe) est en rouge,
La partie { $(x, y) \in ℝ^{2}, tels que y > x^{2}}$ est en rose,
La partie { $(x, y) \in ℝ^{2}, tels que y < x^{2}}$ est en violet.

partition

Union, intersection, complémentaire : définitions

Voici trois opérations importantes dans la théorie des ensembles.

Définition. La réunion de deux sous-ensembles

E

F

d'un ensemble

W

est l'ensemble des éléments de

W

qui appartiennent à

E

ou à

F

(ou aux deux).
La réunion de

E

F

est notée

E \cup F

$E \cup F = {x \in W ∣ x \in E ou x \in F}$

L'ensemble $A \cup B$ est schématisé par la zone grise :

Définition. L'intersection de deux sous-ensembles

E

F

d'un ensemble

W

est l'ensemble des éléments de

W

qui appartiennent à la fois à

E

et à

F

.
L'intersection de

E

F

est notée

E \cap F

$E \cap F = {x \in W ∣ x \in E et x \in F}$

L'ensemble $A \cap B$ est schématisé par la zone grise :

Définition. Si

E

est un sous-ensemble de

W

, le complémentaire de

E

dans

W

est l'ensemble des éléments de

W

qui n'appartiennent pas à

E

.
Le complémentaire de

E

dans

W

est noté

∁_{W} E

. On sous-entend

W

quand il n'y a pas d'ambiguité, on note alors aussi :

E^{c}

\bar{E}

$∁_{W} E = {x \in W ∣ x \in W et x \notin E}$

L'ensemble $A^{c}$ est schématisé par la zone grise :

Exemples et exercices dans la page suivante.

Union, Intersection, complémentaires, exemples, exercices

Exemples.

Pour $W = [- 2, 12] et E = [6, 11]$ , on a $∁_{W} E = [- 2, 6 [\cup] 11, 12]$ .
Si $A$ est une partie de l'ensemble $E$ , alors on a : $A \cap E = A$ et $A \cup \emptyset = A$ .

Exemples graphiques. Sur les figures,

E

est en bleu et

F

en rouge, l'intersection est violette (mélange de rouge et bleu).

Pour $W = [- 2, 12]$ (dessiné en brun), $E$ = [6 , 11] et $F =$ [-1 , 8], la réunion $E \cup F$ est l'intervalle $[- 1, 11]$ (sur la figure $[AB]$ ) et l'intersection $E \cap F$ l'intervalle $[6, 8]$ .

intersection d intervalles

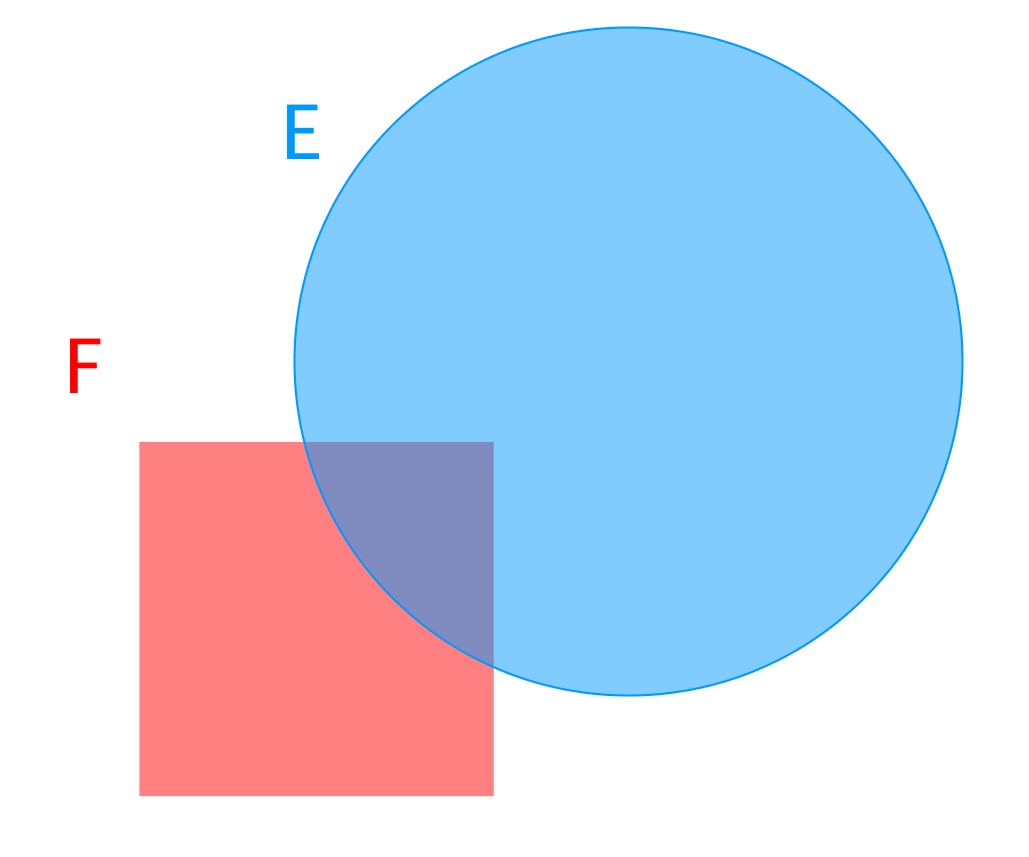
Dans le plan blanc, $E$ est le disque bleu et $F$ le carré rouge ; la réunion $E \cup F$ est la partie colorée du plan, l'intersection $E \cap F$ est la partie violette.

dessin dans le plan

Testez-vous sur ces Exercices .

Différence, différence symétrique

Les opérations définies à la page précédente permettent de définir deux nouvelles opérations :

Définition. La différence de deux sous-ensembles

E

F

d'un ensemble

W

est l'ensemble des éléments de

W

qui appartiennent à

E

et pas à

F

.
La différence de

E

F

est notée

E ∖ F

et se lit " $E$ privé de $F$ ".

$E ∖ F = {x \in W, x \in E$ et $x \notin F}$

On vérifie facilement l'égalité $E ∖ F = E \cap F^{c}$ .

Définition. La différence symétrique de deux sous-ensembles

E

F

d'un ensemble

W

est l'ensemble des éléments de

W

qui appartiennent à

E

et pas à

F

, ou qui appartiennent à

F

et pas à

E

.
La différence symétrique de

E

F

est notée

E Δ F

On vérifie facilement l'égalité : $E Δ F$ = $(E \cup F) ∖ (E \cap F)$ = $(E ∖ F) \cup (F ∖ E)$ .

Testez-vous sur ces Exercices .

Exercices

Il est important de bien comprendre graphiquement de quoi il s'agit. Par exemple, si on vous donne trois sous-ensembles $A$ , $B$ et $C$ d'un ensemble $W$ , savez-vous reconnaître $(A \cup B) \cup C$ ou $(A^{c} \cup B) \cap (C \cup A^{c})$ ?

Exercices.

Complémentaires
Union et intersection
Différence
Opérations combinées
Différence symétrique
Opérations sur des diagrammes
Appartenance/Inclusion et opérations sur les ensembles

Exercices.
Ces exercices en ligne vous permettent de vous entraîner graphiquement aux notions d'union, d'intersection, de complémentaire de sous-ensembles.

Soit on vous présentera graphiquement un sous-ensemble et il vous sera demandé de reconnaitre l'écriture ensembliste correspondante : série 1 ou série 2
Soit on vous donnera une écriture ensembliste à l'aide des opérations d'union, d'intersection et de complémentaire et vous demandera de la reconnaitre graphiquement : Sous-ensembles graphiques

Il y a plusieurs niveaux. Par le lien Intro/configuration , vous pouvez choisir plus simple ou plus compliqué...

Associativité et distributivité

Voici deux propriétés essentielles de la réunion et l'intersection:

Propriétés.

Associativité de l'union, de l'intersection.
Si $E$ , $F$ et $G$ sont trois sous-ensembles de $W$ , les deux égalités suivantes sont vraies :

$E \cup (F \cup G) = (E \cup F) \cup G = E \cup F \cup G$
$E \cap (F \cap G) = (E \cap F) \cap G = E \cap F \cap G$

Distributivité entre union et intersection.
Si $E$ , $F$ et $G$ sont trois sous-ensembles de $W$ , les deux égalités suivantes sont vraies :

$E \cap (F \cup G) = (E \cap F) \cup (E \cap G)$
$E \cup (F \cap G) = (E \cup F) \cap (E \cup G)$

Exercices.

Union, intersection, complémentaire sur des ensembles explicites
Manipulation 1
Manipulation 2

Quelques problèmes concrets

Exercice de modélisation (et distributivité).
Dans une grande librairie, trois employés ont les attributions suivantes :

Jean s'occupe des livres politiques et des romans étrangers reliés.
Pierre s'occupe des livres politiques reliés et des romans anglais qui ne sont pas politiques.
Henri s'occupe des livres anglais et des romans politiques non reliés.

Quels sont les livres sous la compétence des trois employés ? de deux ? d'aucun ?
Mettre le problème sous forme mathématique.

On peut aussi faire un dessin !

Cardinal

Définition. On dit qu'un ensemble est fini lorsqu'il existe un entier naturel

n_{0}

et une bijection de cet ensemble sur [

1, n_{0}

]. Dans le cas contraire, il est dit infini.

Définition. Soit

A

un ensemble fini, on appelle cardinal de

A

, et on le note

Card A

♯ A

, le nombre

n_{0}

d'éléments de

A

. Si

A = ϕ

, alors

Card A = 0

La formule fondamentale pour le calcul des cardinaux d'ensembles finis, est :

$Card (A \cup B) = Card A + Card B - Card (A \cap B)$

Démonstration, pour des ensembles finis

= + = +
= + -

Card (A \cup B) = Card A + Card B - Card (A \cap B)

Propriétés:
Dans ce qui suit

A

B

sont des ensembles finis.

Si $A \subset B$ , alors $Card A \leq Card F$ .
Si $A \subset B$ , et $A \neq B$ , alors $Card A < Card B$
$Card (A \times B) = Card A \times Card B$ .
Si $E$ est un ensemble fini à $n$ éléments c'est-à-dire $Card E = n$ , on note : $𝒫 (E)$ l'ensemble de toutes les parties (de tous les sous-ensembles) de $E$ et on a le résultat : $Card (𝒫 (E)) = 2^{n}$

Cardinaux : exercices pratiques

Exemples et exercices.

Décrire l'ensemble : $𝒫 (𝒫$ ({1}))
Solution
$𝒫$ ({1}) = { $\emptyset, {1}$ }
$𝒫 (𝒫$ ({1}) ) = { $\emptyset$ , ${1}$ , { $\emptyset$ }, { $\emptyset, {1}$ } }
On notera que l'on a noté l'ensemble vide de deux façons, sans accolade lorqu'il s'agit de l'ensemble vide, avec accolade lorsqu'il s'agit de l'élément "ensemble vide", figurant dans $𝒫$ ({1}).
On considère deux sous-ensembles $A$ et $B$ d'un ensemble fini $E$ . On note $n$ (resp. $a, b$ ) le cardinal de $E$ (resp. $A, B$ ). On suppose de plus que $a$ est plus grand que $b$ .
1. Donner un majorant de $Card (A \cup B)$ en fonction de $a$ , $b$ et $n$ . Même question pour $Card (A \cap B)$ .
2. Donner un minorant de $Card (A \cup B)$ en fonction de $a$ , $b$ et $n$ . Même question pour $Card (A \cap B)$ .
Solution
- $Card (A \cup B) \leq Inf (a + b, n)$
- $Card (A \cap B) \leq b$
- $Card (A \cup B) \geq a$
- $Card (A \cap B) \geq Sup (0, a + b - n)$
Utiliser la formule fondamentale deux fois pour donner une formule pour $Card (A \cup B \cup C)$
Solution
$Card (A \cup B \cup C) = Card (A) + Card (B) + Card (C)$
$- Card (A \cap B) - Card (A \cap C) - Card (C \cap B)$
$+ Card (A \cap B \cap C)$
La maîtresse récompense ses élèves avec des caramels ou des bonbons à l'anis (uniquement s'ils ont bien travaillé !). A est l'ensemble des élèves aimant les bonbons à l'anis, C est l'ensemble des élèves aimant les caramels. On donne :
$Card (A \cup C) = 14$ , $Card (A \cap C) = 6$ , $Card C = 8$ , $Card \bar{A} = 17$ .
Quel est l'effectif de la classe ?
(Le lemme des tiroirs) : Montrer que dans le groupe des étudiants de licence, il y au moins deux étudiants qui ont le même nombre d'amis dans ce groupe. On considère qu'on est ami avec soi-même et si Jean est ami avec Pierre, alors Pierre est ami avec Jean.
On rappelle le principe des tiroirs (énoncé par Dirichlet) : si l'on doit mettre $n$ chaussettes dans $p$ tiroirs et que $n > p$ , alors un tiroir contient strictement plus d'une chaussette. En d'autres termes, l'application qui à chaque chaussette associe le tiroir où elle se trouve n'est pas injective.
- Prendre pour premier ensemble l'ensemble des étudiants (de cardinal $n$ ), et pour le second l'ensemble des nombres d'amis que peut avoir chaque étudiant (un nombre nécessairement inférieur ou égal à $n$ ).
- Que se passe-t-il si un étudiant est ami avec tout le monde ? Quelles valeurs $p$ peut-il prendre ?
- Que se passe-t-il si personne n'est ami avec tout le monde ? Quelles valeurs $p$ peut-il prendre ?

Exercice.
Effectifs des classes de langues

cours introductif à la théorie des ensembles.
: union,intersection, différence,cardinal, interactive mathematics, interactive math, server side interactivity

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.