OEF continuità
--- Introduzione ---
Questo modulo contiene per il momento 7 esercizi sulla continuità
(definizione e proprietà fondamentali) di funzioni in una variabile reale.
Funzioni continue ed intervalli
Esiste una funzione continua
tale che l'immagine dell'intervallo
di
è l'intervallo
? Indicare si o no nella tabella qui sotto.
Tra le funzioni seguenti, quale verifica
? Indicare il numero.
-
- linea poligonale che congiunge i punti (,), (,), (,) e (,) seguita dalla semiretta orizzontale di equazione
per
.
-
- linea poligonale che congiunge i punti (,), (, ) e (, ) seguita dalla curva di equazione
-
- linea poligonale che congiunge i punti (,) e (, ) seguita dalla semiretta di equazione
per
- linea poligonale che congiunge i punti
con
se
è un intero pari e
se
è un intero dispari.
- linea poligonale che congiunge i punti (,), (,) e (,)
- linea poligonale che congiunge i punti
con
se
è pari e
se
è un intero dispari
-
- linea poligonale che congiunge i punti
con
se n è un intero pari e
se
è un intero dispari.
-
-
- linea poligonale che congiunge i punti (,), (,), (,) e (,)
-
- linea poligonale che congiunge i punti (,) e (,) e seguita dalla curva di equazione
-
- linea poligonale che congiunge (,) e (,) seguita dalla curva di equazione
- linea poligonale che congiunge i punti
con
se
è un intero relativo pari e maggiore di e
se
è un intero relativo dispari e maggiore di
- linea poligonale che congiunge i punti (,), (, ) seguita dalla semiretta orizzontale
per
- linea poligonale che congiunge i punti
con
se n è un intero relativo pari e maggiore di e
se n è un intero relativo dispari e maggiore di
-
- linea poligonale che congiunge i punti
con
se n è un intero relativo pari e maggiore di e
se n è un intero relativo dispari e maggiore di
-
-
-
-
- la semiretta
fino al punto (,) poi la curva di equazione
- la curva di equazione
fino al punto (,) poi la curva di equazione
- la semiretta di equazione
fino al punto (,), poi la retta di equazione
Continuità e successioni
Sia
una funzione reale. Gli enunciati seguenti sono sempre veri ? A. Se , allora .
B. Se , allora .
Definizione di limite
Con gli elementi seguenti,scrivere che la funzione
ha come limite
con x che tende a
Deve essere scelta una sintassi... Guarda una volta la struttura della risposta (eventualmente disattivando il punteggio).
Epsilon - Delta
Sia
una funzione reale tale che:
Per ogni
, esiste un
tale che
implica
. Cosa significa questo per la continuità di
?
Epsilon - Delta II
Sia
una funzione reale tale che:
Per ogni
, esiste un
tale che
implica
. Cosa significa questo per la continuità di
?
Moltiplicazione mista
Sia
una funzione reale. L'enunciato seguente è correto ? Se
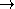 è continua, allora
è continua.
è continua, allora
è continua.
Potenze
Sia
una funzione reale. L'enunciato seguente è corretto ? Se è continua, allora è continua.
- Description: collezione di esercizi sulla continuità di funzioni in una variabile reale. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, analysis, continuite, limite, epsilon, delta, suite,continuità,successione
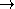 è continua, allora
è continua.
è continua, allora
è continua. 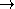 è continua, allora
è continua.
è continua, allora
è continua.