OEF reali
--- Introduzione ---
Questo modulo contiene per il momento 3 esercizi sulla dicotomia.
Dicotomia
Sia
la funzione definita su [,] da
.
L'equazione
ha una soluzione nell'intervallo [,] poiché
,
e
. Indichiamola con
. Si può trovare un valore prossimo a
per dicotomia : Per
, si definisce una successione di interi
uguali a 0 o ad 1 nella maniera seguente
- Si divide l'intervallo [
,
] = [,] in due parti uguali :
[
,
]=[
,
] 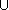 [
,
].
[
,
].
Se
appartiene all'intervallo di destra, vale a dire se
< 0, si pone
, altrimenti,
appartiene all'intervallo di sinistra e si pone
. - E si ricomincia.
Dicotomia inversa
Se
è un reale dell'intervallo [,], si definisce per dicotomia una successione di interi
uguali a 0 o ad 1 nella maniera seguente - Si divide l'intervallo [
,
] = [,] in due parti uguali :
[
,
] = [
,
] 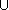 [
,
].
[
,
].
Se
appartiene all'intervallo di destra, si pone
, altrimenti, appartiene all'intervallo di sinistra e si pone
. - E si ricomincia.
Si definisce anche una successione d'interi
. Sia
un reale compreso tra 0 e 1 la cui successione associata
è dopo tappe. Dare il miglior inquadramento di
che si possa trovare a partire da queste informazioni.
Qual è la lunghezza dell'intervallo ottenuto ?
Dicotomia inversa visuale
Se
è un reale dell'intervallo [,], si definisce per dicotomia una successione di interi
uguali a 0 o ad 1 nella maniera seguente - Si divide l'intervallo [
,
] = [,] in due parti uguali :
[
,
] = [
,
] 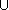 [
,
].
[
,
].
Se
appartiene all'intervallo di destra, si pone
, altrimenti appartiene all'intervallo di sinistra e si pone
. - E si ricomincia.
Si definisce anche una successione di interi
. Calcolare la successione di interi per i reali dell'intervallo in rosso :
xrange -0.2,1.2 yrange -1,1
- Description: collezione di esercizi sulle proprietà dei reali. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, , réel, intermédiaire,dichotomie,reali, intermedio, dicotomia
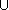 [
,
].
[
,
]. 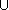 [
,
].
[
,
]. 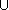 [
,
].
[
,
]. 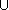 [
,
].
[
,
].