OEF Taylor
--- Introduzione ---
Questo modulo raggruppa per il momento 18 esercizi sullo sviluppo
di Taylor delle funzioni reali di una variabile.
Taylor-ordine
Siano
e
due funzioni aventi come sviluppo di Taylor in 0:
= + ,
= + Fino a che ordine è possibile calcolare lo sviluppo di Taylor di
in 0 ? Rispondere nessuno se questo non è possibile.
DL-ordre+
Soient
et
deux fonctions admettant les développements limités suivants en 0 :
= + ,
= + A quel ordre peut-on calculer le développement limité de
en 0 ?
DL-ordrex
Soient
et
deux fonctions admettant les développements limités suivants en 0 :
= + ,
= + A quel ordre peut-on calculer le développement limité de
en 0 ? Répondre non si cela n'est pas possible.
DL-ordre-compos0
Soient
et
deux fonctions admettant les développements limités suivants respectivement en et en :
Peut-on calculer un développement limité de
en ?
DL-ordre-compos*
Soient
et
deux fonctions admettant les développements limités suivants respectivement en et en :
A quel ordre peut-on calculer le développement limité de
en ? Répondre -1 si les renseignements fournis ne sont pas suffisants pour pouvoir calculer un développement limité en .
Derivata I
Sia
una funzione derivabile fino al terzo ordine e avente come sviluppo di Taylor
= in un intorno di . Quanto vale la derivata d'ordine di
nel punto ?
Derivata II
Sia una funzione su 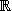 , e supponiamo che si possa scrivere
= .
, e supponiamo che si possa scrivere
= . Dall'espressione precedente è possibile dedurre che è derivabile in un certo punto
. Dire qual è il valore di
e quello di (
) .
Sviluppo di Taylor e notazioni 1
Sia f una funzione che in un intorno di 0 può essere scritta nella forma
.
Di che ordine è lo sviluppo di Taylor di f in un intorno dell'origine?
Sviluppo di Taylor e notazioni II
Sia
una funzione che in un intorno di 0 può essere scritta della forma,
.
Dire se la seguente affermazione è corretta:
Stima dell'errore I
La funzione
è derivabile fino al quarto ordine nell'intervallo [,] e ammette il seguente sviluppo di Taylor
= in un intorno di 0. Si suppone che
su [,]. Calcolare qual è il massimo errore che si commette rimpiazzando
con su [,].
Stima dell'errore II
La funzione
è derivabile fino all'ordine nell'intervallo [,] e ammette il seguente sviluppo di Taylor
= in un intorno di . Supponendo che valga
in questo intervallo, qual è il massimo errore che si commette rimpiazzando
con
su [,] ?
Stima dell'errore III
La fonction
è derivabile fino al quarto ordine su 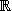 e ammette il seguente sviluppo di Taylor
=
e ammette il seguente sviluppo di Taylor
= in un intorno di 0. Supponiamo che valga
. Vogliamo rimpiazzare
con nell'intervallo
senza introdurre un errore superiore a . Qual è il valore massimo di
che possiamo usare?
Tabella 2
Sia una funzione reale, derivabile fino al terzo ordine su 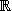 , con la seguente tabella delle derivate:
, con la seguente tabella delle derivate: Quale è la parte principale dello sviluppo di Taylor di d'ordine 2 in un intorno di , cioè il polinomio P(x) nello sviluppo di Taylor
(x) = P(x) + o(()2) ?
Tabella 3
Sia una funzione reale, derivabile fino al terzo ordine su 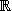 , con la seguente tabella delle derivate:
, con la seguente tabella delle derivate: Qual è la parte principale dello sviluppo di Taylor di d'ordine 3 in un intorno di , cioè il polinomio P(x) nello sviluppo di Taylor
(x) = P(x) + o(()3) ?
Tangente
La funzione ammette nell'intorno di lo sviluppo di Taylor (x) = Indichiamo con il grafico di e con la tangente a nel punto (, ()). Qual è la posizione del grafico di rispetto a nell'intorno di ?
- sta sotto .
- sta sopra .
- sta sotto a sinistra (quando
< ), e sopra a destra (quando
> ).
- sta sopra a sinistra, e sotto à droite.
Formula di Taylor 2
Sia
una funzione
su
a valori reali.
Scrivere la formula di Taylor- di ordine 2 nel punto
(si suppone che
sia un punto tale che
e
una funzione che tende a 0 per
che tende a ):
I termini devono essere scritti nell'ordine standard!
Effettivamente la formula di Taylor- di ordine 2 nel punto
è della forma
con
una funzione che tende a 0 per
che tende a
con
un numero reale compreso tra
e
. Sia
la funzione affine definita da
. Supponendo che
per ogni
tale che
.
Con queste ipotesi, è possibile utlizzare la formula di Taylor data per dare una maggiorazione di
pour
? Se sì, dare la migliore maggiorazione possibile. Altrimenti, rispondere no
Valore
Sia una funzione definita su 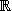 e supponiamo che si possa scrivere
= .
e supponiamo che si possa scrivere
= . Dall'espressione precedente è possibile dedurre il valore esatto di in un punto
. Dire qual è il valore di
e quello di
.
Valore II
Sia una funzione reale, e supponiamo che si possa scrivere (x) = . Dall'espressione precedente è possibile dedurre che è derivabile in un certo punto
. Dire qual è il valore di
e quello di
.
- Description: collezione di esercizi sullo sviluppo di Taylor di una funzione reale. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, analysis, calculus, Taylor, function, derivative, integral, differential equation, fonction, développement limité, dérivée, intégrale, équation différentielle, funzione, sviluppo di Taylor, derivata, integrale, equazione differenziale
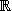 , e supponiamo che si possa scrivere
, e supponiamo che si possa scrivere 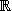 e ammette il seguente sviluppo di Taylor
e ammette il seguente sviluppo di Taylor 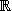 , con la seguente tabella delle derivate:
, con la seguente tabella delle derivate: 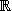 , con la seguente tabella delle derivate:
, con la seguente tabella delle derivate: 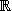 e supponiamo che si possa scrivere
e supponiamo che si possa scrivere