Sapere minimo di matematica
--- Introduzione ---
Questo modulo al momento contiene 108 esercizi su ...
00 Aree settori circolari
Sia
il cerchio con centro in
e raggio .
Sia
il sottoinsieme di
costituito dai punti che con le loro coordinate soddisfano la relazione
.
Allora l'area di
vale:
DisEq.Trig.Quadrato
La disequazione ammette come soluzioni:
Diseq 1
La disequazione (
4-)2 > 0 ammette le seguenti soluzioni:
Diseq 2
La disequazione
4 -
4 + < 0 ammette le seguenti soluzioni:
Diseq 3
La disequazione irrazionale √
0 ammette le seguenti soluzioni:
Disequazioni Intere
La disequazione
0 è verificata per:
Disequazioni con un quoziente
| Risolvere algebricamente su
la disequazione (1) : |
-
La disequazione (1) è equivalente alla disequazione
con
e
binomi di primo grado che soddisfano :
=
e
=
Ora risolvere la disequazione (1) equivale a risolvere la disequazione (2) :
- Studiando la tabella dei segni di
in funzione di
si ottiene la tabella seguente :
- Definiamo i seguenti intervalli : Guardando la tabella dei segni la soluzione di (1) e (2) vale :
00 Duplicazione/bisezione
Sapendo che
quanto vale ?
Eq.SinCos
L'equazione sin x = cos x
Eq.Sin.Reali
Determinare i valori reali di x che soddisfano l'equazione:
Eq.Tang.
Data l'equazione
=
stabilire la risposta corretta.
Eq.Trig.Quadrante
Se consideriamo allora è uguale a:
Eq.Trig.Quadrato
L'equazione ()
ha per soluzioni:
Eq.tan x
Data l'equazione
stabilire la risposta corretta.
Equazione(1)
Sia data l'equazione di primo grado della forma:
, con l'aggiunta della condizione . Quale affermazione è corretta?
Equazioni di secondo grado
Sia
la radice positiva dell'equazione
=0 Allora
vale:
Equazioni irrazionali 1
L'equazione √
2 - = √ -
2 - è definita:
Equazioni irrazionali 2
L'equazione √ -
2 - =
+ non può ammettere soluzioni reali perché:
Equazioni irrazionali 3
L'equazione √
4 +
2 + = 0 non può ammettere soluzioni reali perché:
Equazioni irrazionali 1 (czz)
L'equazione √
2 - = √ -
2 - è definita: ,$m_le,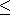
Es11
Sia a>0. L'espressione
vale
Es12:Polinomi
Il polinomio
Es13:Disequazioni2
La disequazione 0 è verificata per:
Es13:Disequazioni2bis
La disequazione 0 è verificata per:
Es13:Disequazioni2
La disequazione 0 è verificata per:
Es14:Frazioni di polinomi
L'espressione
Es15:Frazioni di polinomi2
L'espressione
Es16
Sia
. Allora
vale
Es5:Disequazioni
La disequazione
0 è verificata per:
Es8
Siano
e
due numeri naturali primi tra loro. Denotiamo con M.C.D.(a,b) il massimo comun divisore tra
e
. Allora:
Es 9-10
La seguente affermazione è
Esponenziali 1
vale
Esponenziali 2
Sia
. Quale di queste uguaglianze è FALSA?
Esponenziali 3
La disequazione
è verificata se e solo se
Esponenziali 4
Quale di queste funzioni assume solo valori negativi?
Esponenziali 5
L’equazione x+-x=0
Esponenziali 6
Sia
un numero positivo diverso da 1. L’equazione
=0 ha
Esponenziali 7
Sia a > 1. Quale di queste uguaglianze è FALSA ?
Esponenziali 8
Quale di queste uguaglianze è VERA ?
Exp1
L'equazione esponenziale
ha soluzione:
Exp2
L' equazione
ammette come soluzioni:
Exp3
L'espressione
1000 -
non è uguale a:
Exp4
L'espressione
è uguale a:
Frazioni di polinomi
L'espressione
Geometria Analitica 2
L'equazione y
+m(x+) rappresenta, al variare di m
Geometria Analitica 1 bis
La retta passante per (,) e parallela alla retta di equazione ha equazione
Geometria Analitica 9
L'equazione y=
x+c rappresenta un insieme di parabole. Quale delle seguenti deduzioni è errata? Le parabole di questo insieme hanno
Geometria Analitica 10
Quale dei grafici seguenti è quello della parabola nella cui equazione a 0, c 0?
Geometria Analitica 11
Quale dei grafici seguenti è quello della parabola nella cui equazione
-4ac 0, a 0, c 0?
Geometria Analitica 12
Scrivere l'equazione del luogo geometrico dei punti P del piano tali che la somma delle distanze di P dai punti (-,0) e (,0) sia .
Geometria Analitica 13
Scrivere l'equazione del luogo geometrico dei punti P del piano tali che la differenza delle distanze di P dai punti (-,0) e (,0) sia .
Geometria Analitica 1
La retta passante per (,) e perpendicolare alla retta di equazione ha equazione
Geometria Analitica 4
La retta passante per i punti (,) e (,) ha equazione
Geometria Analitica 5
La retta passante per i punti (,) e (,) ha equazione
Geometria Analitica 3
La retta passante per i punti (,) e (,) ha equazione
Geometria Analitica 6
L'equazione rappresenta
Geometria Analitica 8
Quale di queste affermazioni è vera?
Geometria Analitica 7
Quale di queste affermazioni è falsa?
Geometria Analitica 7-8
La seguente affermazione è
Iperbole
Fra i seguenti disegni, quale rappresenta l'iperbole di equazione
Fra le seguenti equazioni, quale rappresenta il disegno dell'iperbole:
Determina le equazioni degli asintoti dell'iperbole d'equazione
,
Scrivere per primo l'equazione dell'asintoto con pendenza positiva.
Logaritmi 1
L'equazione
è soddisfatta per
Logaritmi 2
L'equazione
è soddisfatta per
Logaritmi 3
L'equazione =0 è soddisfatta per
Logaritmi 4
L'espressione
, dove è definita, è uguale a
Logaritmi 5
La disequazione
, è verificata
Logaritmi 6
L'espressione x y vale
Logaritmi 7
La seguente affermazione è
00 Negazione
Si consideri la seguente affermazione:
. La sua negazione è:
00 Condizioni necessarie e sufficienti
Siano A e B due proposizioni di cui si sa che se
. Quale di questi affermazioni è corretta?
00 Insiemi
00 Condizioni necessarie e sufficienti 2
Si considerino queste due affermazioni:
Allora
Moduli 1
L'equazione |
+| + |
-| = 0 ammette come soluzioni:
Moduli 2
L'equazione |
-| + |
2-| = 0 ammette come soluzioni:
Moduli 3
L'equazione |
2-| = - ammette come soluzioni:
Moduli 4
L'equazione
ammette come soluzioni:
Moduli 5
La disequazione |
-| > 0 ammette come soluzioni:
Moduli 6
La disequazione |
2-
| > -|
| ammette come soluzioni:
Moduli 7
La disequazione |
2-| < 0 ammette come soluzioni:
Parabola
Fra i seguenti disegni, quale rappresenta la parabola di equazione
Fra le seguenti equazioni, quale rappresenta il disegno della parabola:
Parabola a passi
Data la parabola y= x2+ ed il punto P(, ) determinare l'equazione della retta tangente alla parabola e passante per il punto P.
Comincia con lo scrivere l'equazione della generica retta passante per P. y-
=m(x-
)
BENE!
Ora, qual è la condizione di tangenza tra la parabola y= x2+ e la retta y-()=m(x-())?
Quindi, la retta y-()=m(x-()) è tangente alla parabola y= x2+ se e solo se m=
Segno di polinomi
| Stabilire il segno di
dipendente da
è
. |
Polinomi(6)
Dato il polinomio:
stabilire la risposta falsa.
Eq.Trig.Immediate
Data l'equazione
stabilire la risposta corretta.
Polinomi(7)
Dato il polinomio:
stabilire la risposta falsa.
Polinomio(19)
Dato il polinomio:
è divisibile per.
Polinomio(20)
Dato il polinomio:
è equivalente a:
Prodotto di monomi
| Utilizzando la tabella dei segni, risolvere in
, la disequazione
e dare la soluzione sotto forma di intervallo o di unione di intervalli. |
Quanto vale?
La seguente frazione
vale?
00 Radiante
Radicale I
Risolvere la disequazione
Radicale II
Risolvere la disequazione
Radicale III
Risolvere la disequazione
Es4:Radicali
Quali delle seguenti affermazioni è vera?
00 Seno e Coseno
Se
è un generico valore nell'intervallo , allora è uguale a:
Retta a passi
Dati due punti P1(,) e P2(,) determina l'equazione della retta passante per questi due punti.
Qual è l'equazione del fascio di rette passanti per P1 al variare di m? y-
=m(x-
)
BRAVO! Hai correttamente individuato che il fascio di rette passanti per P1(,) è =m (). A questo punto determina m per trovare la retta del fascio che passa anche per P2(,). Qual'è il valore di m? m=
Retta per due punti a passi
Dati due punti P1(,) e P2(,) determina l'equazione della retta passante per questi due punti.
Qual è l'equazione del fascio di rette passanti per P1 al variare di m? y-
=m(x-
)
BRAVO! Hai correttamente individuato che il fascio di rette passanti per P1(,) è =m (). A questo punto determina m per trovare la retta del fascio che passa anche per P2(,). Qual'è il valore di m? m=
Segno di un binomio
| Costruire la tabella dei segni di
definita su 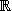 per
. per
. |
Semplificare
La frazione
vale
Coefficiente angolare
Calcolare il coefficiente angolare della retta passante per i punti
e
00 Triangoli generici
.
Quale di queste affermazioni è ?
00 Triangoli rettangoli (sen e cos)
In un triangolo rettangolo l'ipotenusa misura cm. Sapendo = , dove  è uno dei due angoli acuti, i due lati misurano (in centimetri):
è uno dei due angoli acuti, i due lati misurano (in centimetri):
00 Triangoli rettangoli (tan)
In un triangolo rettangolo il cateto maggiore BC misura cm. Sapendo che
, dove  è l'angolo opposto a BC, l'ipotenusa AC misura (in centimetri):
è l'angolo opposto a BC, l'ipotenusa AC misura (in centimetri):
00 Triangoli rettangoli
Un triangolo rettangolo ha un angolo di e l'ipotenusa misura cm. Quanto misura il cateto (in centimetri)?
Triangolo Ottuso
Sia T un triangolo con un angolo ottuso  . Quale di queste affermazioni è falsa?
. Quale di queste affermazioni è falsa?
Trigonometria 1
La seguente affermazione è
Vero o falso
La seguente affermazione è
logica(11)
se si denota con AC (rispettivamente BC ) il complementare di A (B), quale delle seguenti affermazioni è vera:
logica(6)
Sia X un sottoinsieme proprio di Y. Quale di queste affermazioni è falsa?
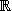 per
.
per
. 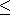
 è uno dei due angoli acuti, i due lati misurano (in centimetri):
è uno dei due angoli acuti, i due lati misurano (in centimetri):  è l'angolo opposto a BC, l'ipotenusa AC misura (in centimetri):
è l'angolo opposto a BC, l'ipotenusa AC misura (in centimetri): . Quale di queste affermazioni è falsa?
. Quale di queste affermazioni è falsa?